Social Sciences
Here I'll follow up on the idea of using an epidemiological model to capture the effects of political mobilization through organization. One of the sample models provided by the NetLogo library is EpiDEM Basic (link). This model simulates an infectious disease moving through a population through person-to-person contact.
We can adapt this model to a political context by understanding "infection" as "recruitment to the party". I've modified the model to allow for re-infection after an agent has been cured [disaffiliated from the party]. This corresponds to exit and re-entrance into a party or political organization. This leads the model to reach various levels of equilibrium within the population depending on the settings chosen for infectiousness, cure rates, and cure time frames. The video above represents a sample run of my extension of EpiDEM Basic. The graph represents the percentage of the population that have been recruited to the party at each iteration. The infection rate [mobilization success] surges to nearly 100% in the early ticks of the model, but then settles down to a rough equilibrium for the duration of the run. Orange figures are party members, while blue are not members (either because they have never affiliated or they have dis-affiliated).
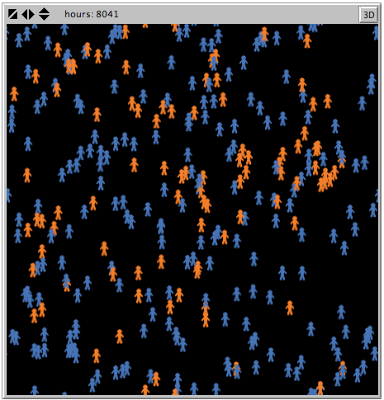
An important shortcoming in this approach is that it is forced to represent every agent as a "cadre" for the organization as soon as he/she is recruited; whereas on the ground it is generally a much smaller set of professional cadres who serve as the vectors of proselytization for the party. This accounts for the early surge in membership to almost 100%, which then moderates to the 30% level. The initial surge derives from the exponential spread of infection prior to the period in which cures begin to occur. I've referenced this flaw in the realism of the model by calling this a "grassroots" party. On the current settings of recruitment and defection the population stabilizes at about 30% membership in the party. Ideally the model could be further modified to incorporate "infection" by only a specified set of cadres rather than all members.
It seems possible to merge this party-mobilization model with the Epstein model of rebellion (also provided in the NetLogo library), allowing us taking party membership into account as a factor in activation. In other words, we could attempt to model two processes simultaneously: the "infection" of new party members through a contagion model, and the differential activation of agents according to whether they are exposed to a party member or not. This is complicated, though, and there is a simpler way of proceeding: try to represent the workings of the model with an exogenously given number of party cadres. This can be implemented very simply into the Epstein Rebellion model.
As a first step, I introduce party membership as a fixed percentage of population and assume that the threshold for activation is substantially lower for members than non-members. The causal assumption is this: the presence of a party member in a neighborhood increases the threshold for action. The logic of this modification is this: for a given agent, if there is a party member in the neighborhood, then the threshold for action is low; whereas if there is no party member in the neighborhood, the threshold for action is high.
Now run the model with two sets of assumptions: no party members and 1% party members.
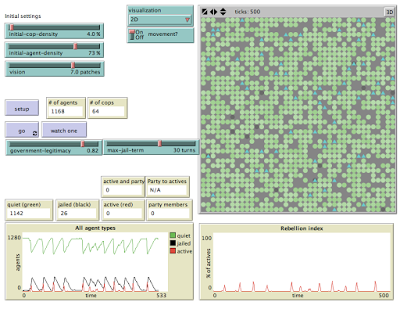
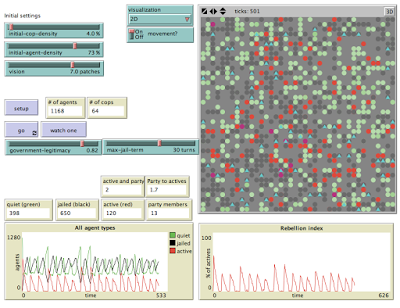
The two panels represent these two scenarios. As the two panels illustrate, the behavior of the population of agents is substantially different in the two cases. In both scenarios there are sudden peaks of activism (measured on the "Rebellion Index" panel). But those peaks are both higher and more frequent in the presents of a small number of activists. So we might say the model succeeds in illustrating the difference that organization makes in the occurrence of mobilization. A few party activists substantially increase the likelihood of rebellion.
Or does it? Probably not.
The modifications introduced here are very simple, and they succeed in addressing a primary concern I raised in an earlier post about the original version of Epstein's model: the fact that it does not take the presence of organization into account as a causal factor in civil unrest. But the realism of the model is still low. For example, the Rebellion model is specifically intended to capture the relationship between cops and agents. But it is not interactive in the other way in which rebellious behavior spreads: the process in which rising density of activation in a neighborhood increases the probability of activation for each individual. In other words, neither the original implementation nor this simple extension allows introduction of the spatial dimensions of mobilization and civil unrest (aside from the original random location of party activists).
But most fundamentally, the extension I've presented here is still a highly abstract representation of the workings of organizations in the context of civil unrest and mobilization. I've boiled the workings of a political organization down to a single effect: if a neighborhood is exposed to a party cadre, the individuals in that neighborhood are substantially more likely to become active. And the model behaves accordingly; there is more activism when there are more cadres. But we can't really interpret this as the derivation of a social effect from an independent set of assumptions; rather, the implementation of the idea of organization simply assumes the fact that cadres amplify activation by others in the neighborhood. In other words, the model is built to embody the effect I was expecting to see.
This exercise makes a couple of points. First, agent-based models have the virtue of being very explicit about the logic of action that is represented. So it is possible for anyone to review the code and to modify the assumptions, or to introduce factors that perhaps should be considered. (NetLogo is particularly welcoming to the non-expert in this regard, since it is easy to go back and forth between the code and the graphical representation of the model.)
But second, no one should imagine that agent-based models reproduce reality. Any ABM is implemented by (1) codifying one or more assumptions about the factors that influence a given collective phenomenon, and (2) codifying the rules of action for the kinds of agents that are to be represented. Both kinds of assumption require extreme abstraction from the reality of a social setting, and therefore models can almost invariably be challenged for a lack of realism. It is hard for me to see how an agent-based model might be thought to be explanatory of a complex social reality such as the Cairo uprising.
- Abm Approaches To Social Conflict
Source: Pfautz and Salwen (link) An earlier post addressed the question of the dynamics through which a stable community consisting of multiple groups may begin to polarize and fission into antagonisms and conflict. I speculated there that the tools of...
- Social Mechanisms And Abm Methods
One particularly appealing aspect of agent-based models is the role they can play in demonstrating the inner workings of a major class of social mechanisms, the group we might refer to as mechanisms of aggregation. An ABM is designed to work out how...
- Computational Models For Social Phenomena
There is a very lively body of work emerging in the intersection between computational mathematics and various fields of the social sciences. This emerging synergy between advanced computational mathematics and the social sciences is possible, in part,...
- Social Upheaval
image: Monte Carlo simulation of portfolio value We sometimes think that there is fundamental stability in the social world, or at least an orderly pattern of development to the large social changes that occur. When there are crises -- like the financial...
- North Korea Rock Party
Tip of the hat for the above find to a former APP research assistant who will remain unnamed as he is a PhD candidate at Harvard University. As the creator of the above video says "Ain't no party like a? Pyongyang party, 'cause a Pyongyang party...
Social Sciences
Modifying an epidemiological model for party recruitment
We can adapt this model to a political context by understanding "infection" as "recruitment to the party". I've modified the model to allow for re-infection after an agent has been cured [disaffiliated from the party]. This corresponds to exit and re-entrance into a party or political organization. This leads the model to reach various levels of equilibrium within the population depending on the settings chosen for infectiousness, cure rates, and cure time frames. The video above represents a sample run of my extension of EpiDEM Basic. The graph represents the percentage of the population that have been recruited to the party at each iteration. The infection rate [mobilization success] surges to nearly 100% in the early ticks of the model, but then settles down to a rough equilibrium for the duration of the run. Orange figures are party members, while blue are not members (either because they have never affiliated or they have dis-affiliated).

An important shortcoming in this approach is that it is forced to represent every agent as a "cadre" for the organization as soon as he/she is recruited; whereas on the ground it is generally a much smaller set of professional cadres who serve as the vectors of proselytization for the party. This accounts for the early surge in membership to almost 100%, which then moderates to the 30% level. The initial surge derives from the exponential spread of infection prior to the period in which cures begin to occur. I've referenced this flaw in the realism of the model by calling this a "grassroots" party. On the current settings of recruitment and defection the population stabilizes at about 30% membership in the party. Ideally the model could be further modified to incorporate "infection" by only a specified set of cadres rather than all members.
It seems possible to merge this party-mobilization model with the Epstein model of rebellion (also provided in the NetLogo library), allowing us taking party membership into account as a factor in activation. In other words, we could attempt to model two processes simultaneously: the "infection" of new party members through a contagion model, and the differential activation of agents according to whether they are exposed to a party member or not. This is complicated, though, and there is a simpler way of proceeding: try to represent the workings of the model with an exogenously given number of party cadres. This can be implemented very simply into the Epstein Rebellion model.
As a first step, I introduce party membership as a fixed percentage of population and assume that the threshold for activation is substantially lower for members than non-members. The causal assumption is this: the presence of a party member in a neighborhood increases the threshold for action. The logic of this modification is this: for a given agent, if there is a party member in the neighborhood, then the threshold for action is low; whereas if there is no party member in the neighborhood, the threshold for action is high.
Now run the model with two sets of assumptions: no party members and 1% party members.

Scenario 1: occurrence of mobilization with no party members

Scenario 2: occurrence of mobilization with 1% party members
The two panels represent these two scenarios. As the two panels illustrate, the behavior of the population of agents is substantially different in the two cases. In both scenarios there are sudden peaks of activism (measured on the "Rebellion Index" panel). But those peaks are both higher and more frequent in the presents of a small number of activists. So we might say the model succeeds in illustrating the difference that organization makes in the occurrence of mobilization. A few party activists substantially increase the likelihood of rebellion.
Or does it? Probably not.
The modifications introduced here are very simple, and they succeed in addressing a primary concern I raised in an earlier post about the original version of Epstein's model: the fact that it does not take the presence of organization into account as a causal factor in civil unrest. But the realism of the model is still low. For example, the Rebellion model is specifically intended to capture the relationship between cops and agents. But it is not interactive in the other way in which rebellious behavior spreads: the process in which rising density of activation in a neighborhood increases the probability of activation for each individual. In other words, neither the original implementation nor this simple extension allows introduction of the spatial dimensions of mobilization and civil unrest (aside from the original random location of party activists).
But most fundamentally, the extension I've presented here is still a highly abstract representation of the workings of organizations in the context of civil unrest and mobilization. I've boiled the workings of a political organization down to a single effect: if a neighborhood is exposed to a party cadre, the individuals in that neighborhood are substantially more likely to become active. And the model behaves accordingly; there is more activism when there are more cadres. But we can't really interpret this as the derivation of a social effect from an independent set of assumptions; rather, the implementation of the idea of organization simply assumes the fact that cadres amplify activation by others in the neighborhood. In other words, the model is built to embody the effect I was expecting to see.
This exercise makes a couple of points. First, agent-based models have the virtue of being very explicit about the logic of action that is represented. So it is possible for anyone to review the code and to modify the assumptions, or to introduce factors that perhaps should be considered. (NetLogo is particularly welcoming to the non-expert in this regard, since it is easy to go back and forth between the code and the graphical representation of the model.)
But second, no one should imagine that agent-based models reproduce reality. Any ABM is implemented by (1) codifying one or more assumptions about the factors that influence a given collective phenomenon, and (2) codifying the rules of action for the kinds of agents that are to be represented. Both kinds of assumption require extreme abstraction from the reality of a social setting, and therefore models can almost invariably be challenged for a lack of realism. It is hard for me to see how an agent-based model might be thought to be explanatory of a complex social reality such as the Cairo uprising.
- Abm Approaches To Social Conflict
Source: Pfautz and Salwen (link) An earlier post addressed the question of the dynamics through which a stable community consisting of multiple groups may begin to polarize and fission into antagonisms and conflict. I speculated there that the tools of...
- Social Mechanisms And Abm Methods
One particularly appealing aspect of agent-based models is the role they can play in demonstrating the inner workings of a major class of social mechanisms, the group we might refer to as mechanisms of aggregation. An ABM is designed to work out how...
- Computational Models For Social Phenomena
There is a very lively body of work emerging in the intersection between computational mathematics and various fields of the social sciences. This emerging synergy between advanced computational mathematics and the social sciences is possible, in part,...
- Social Upheaval
image: Monte Carlo simulation of portfolio value We sometimes think that there is fundamental stability in the social world, or at least an orderly pattern of development to the large social changes that occur. When there are crises -- like the financial...
- North Korea Rock Party
Tip of the hat for the above find to a former APP research assistant who will remain unnamed as he is a PhD candidate at Harvard University. As the creator of the above video says "Ain't no party like a? Pyongyang party, 'cause a Pyongyang party...
